如何基于双LCC实现电动汽车多阶段恒流蓄电池充电机无线充电技术?
2018-5-9 13:42:13 点击:
电动汽车作为一种新能源汽车,以其污染小、噪音低等优点,得到国际和国内社会的广泛认可和支持,随着社会的不断发展和科技的不断进步,电动汽车的充电方式也从传统的充电机有线充电模式向蓄电池充电机无线充电模式过渡。相较于有线充电方式,蓄电池充电机无线充电具有方便、安全、操作简单及无机械磨损等优点,得到广泛关注和研究。
但是,目前电动汽车的蓄电池充电机无线充电多为恒流充电,而恒流充电尽快可以较为快速的为动力电池补充能量,但是在充电的后期会造成电池严重的极化现象,进而缩短动力电池的使用寿命。
针对这个问题,本文提出了基于LCC的电动汽车多阶段恒流蓄电池充电机无线充电技术,随着动力电池的电量的上升,减小动力电池的充电电流的大小,进而使得动力电池的充电电流较为接近动力电池的最佳充电曲线,进而可以减少对动力电池的损害,延长其使用寿命,降低电动汽车的使用成本,且可以降低动力电池的更换频率,进而对环境更友好。
技术原理
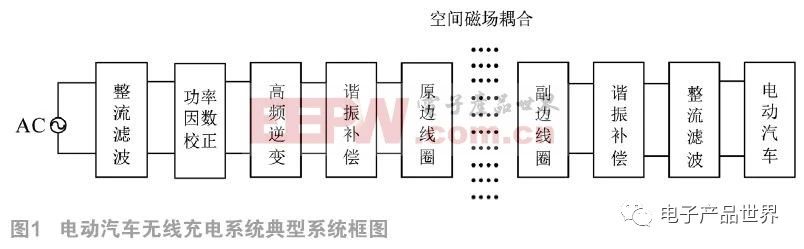
三相交流电或者单相交流电经工频整流滤波电路和功率因数校正电路变换成直流电,经高频逆变电路变换成高频交流电,注入到由谐振补偿电路和原边线圈构成的谐振网络,在原边线圈周围产生高频交变磁场,副边线圈在高频交变磁场中感应出高频交流电,经谐振补偿电路和整流滤波电路之后为电动汽车充电。
多阶段恒流充电
多阶段恒流充电示意图如图2所示,从图中可以看出充电过程分为若干个阶段,且从初始阶段到最终阶段电流是依次减小的,且电流越大,充电时间越短;电流越小,对应的阶段充电时间越长。
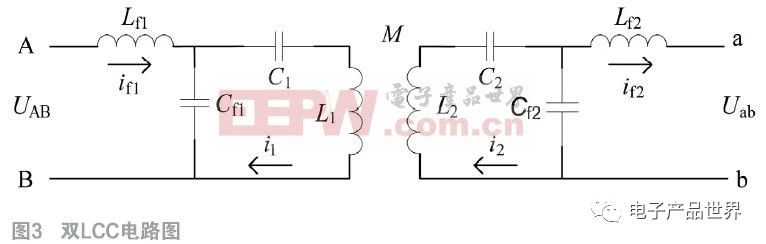
将动力电池的充电阶段分的越多,动力电池的充电电流便越接近于最佳充电曲线,对电池的损害便越小,更有利于延长动力电池的使用寿命。若动力电池为锂电池,最后阶段的电流一般为电池组容量的0.05倍,当电池电压达到截止电压便可以停止充电。
双LCC谐振补偿拓扑
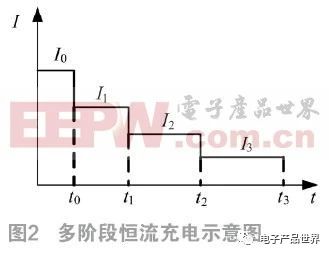
如图3所示L1是原边线圈感值,L2是副边线圈感值,C1、Cf1和Lf1是原边补偿电感和电容,C2、Cf2和Lf2是副边补偿电感和电容,UAB是逆变器的输出电压和Uab是副边补偿拓扑的输出电压,M是原副边线圈互感。i1、i2、if1和if2分别是线圈L1、L2、Lf1、Lf2的电流。
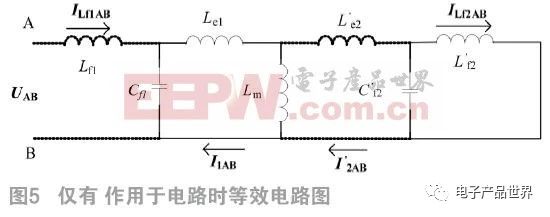
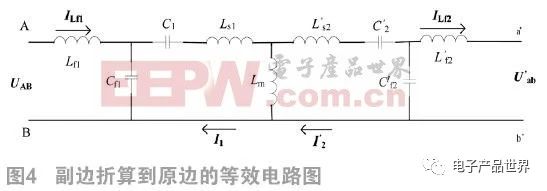
电动汽车蓄电池充电机无线充电系统中的磁路机构是一个松耦合变压器,故可将图3中的副边电感电容折算到原边,得到如图4所示的等效电路图。为了简化分析,忽略电感电容的内阻,且只考虑逆变器输出电压的基波。定义松耦合变压器的变比n为:
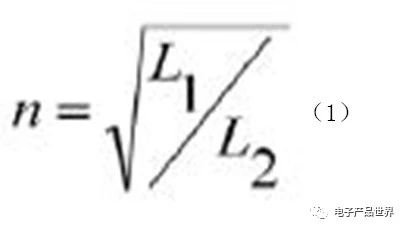
图4中的变量可由公式(2)表达:
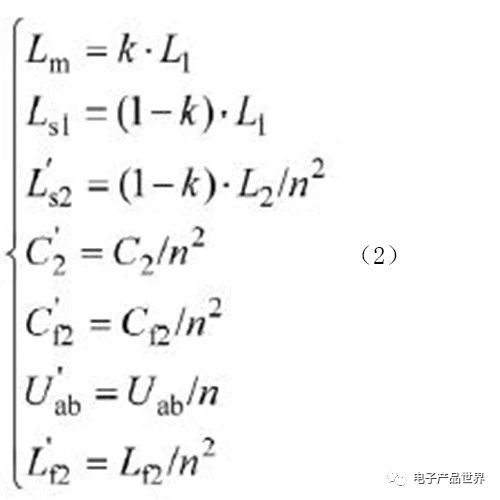
其中Lm为折算到原边的励磁电感。对于如图2所示的高阶系统,其谐振频率有多个,本文重点研究LCC的电压电流特性,不研究其频域特性,故本文将系统的工作频率设定为一个固定的谐振频率。电路谐振状态下,逆变器的输出电压和输出电流是同相位的,由公式(3)可计算电路的谐振频率。

此处的ω0是补偿电路的固有谐振角频率,从式(3)中可看出角频率只与电路中的电感电容有关,而与负载、原副边的互感无关。下文设定的频率均为固定的谐振角频率。
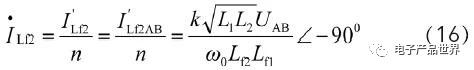



从式(3)可知,双LCC可以在动力电池充电的全过程以及耦合系数发生变化的情况下保持谐振状态,此性能非常符合电动汽车的蓄电池充电机无线充电的应用背景,因为动力电池充电过程中其等效电阻会不断增大,且每次充电原副边线圈会存在不同程度的偏移,故每次充电的耦合系数也是不同的。
由式(16)可知,双LCC补偿拓客可以实现恒流输出,且其输出电流的大小与逆变器的输出电压成正比,故可控制逆变器的输出电压来调节动力电池的充电电流,实现动力电池的多阶段恒流充电。
仿真验证
在MATLAB/Simulink中搭建仿真电路,电路参数表1所示。
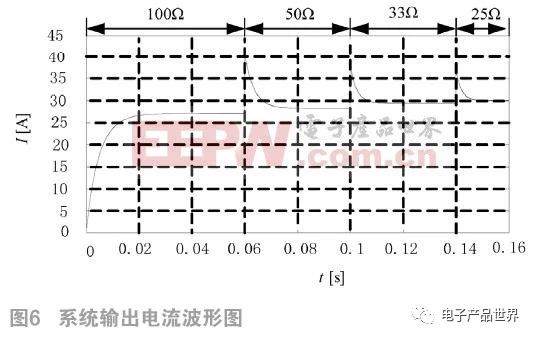
图6为系统输出电流波形图。在0.06 s、0.1 s,0.14 s切换电阻,阻值依次为100 Ω、50 Ω、33 Ω及25 Ω,从图6中可得:电阻变化前后,电流几乎不变。电阻切换时出现震荡,在短时间内会稳定在某一固定值。动力电池充电时,可认为其等效内阻在一定时间内不变,故不会产生图7中所示的震荡。
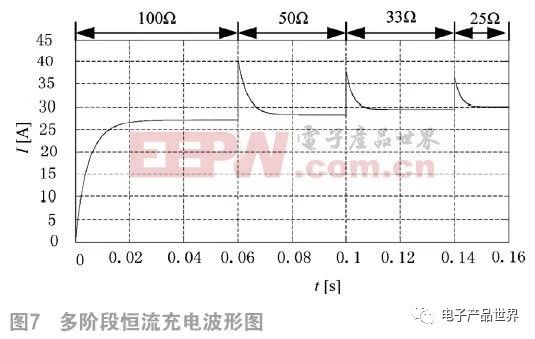
图8为动力电池组不同的电量时对应的充电电流,因为在电脑中模拟的时间长度有限,故在仿真时每个阶段容量设置为0.005 C。
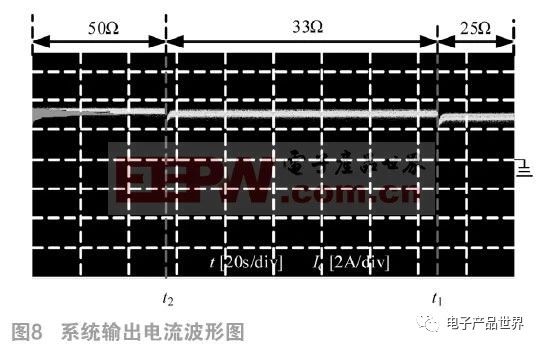
在t1时刻将电阻由25 Ω切换到33 Ω;在t2时刻将电阻由33 Ω切换到50 Ω,得到如图7所示的系统输出电流,可看出电阻切换前后电流大小几乎不变,可以用来实现电动汽车的多阶段恒流充电。
但是,目前电动汽车的蓄电池充电机无线充电多为恒流充电,而恒流充电尽快可以较为快速的为动力电池补充能量,但是在充电的后期会造成电池严重的极化现象,进而缩短动力电池的使用寿命。
针对这个问题,本文提出了基于LCC的电动汽车多阶段恒流蓄电池充电机无线充电技术,随着动力电池的电量的上升,减小动力电池的充电电流的大小,进而使得动力电池的充电电流较为接近动力电池的最佳充电曲线,进而可以减少对动力电池的损害,延长其使用寿命,降低电动汽车的使用成本,且可以降低动力电池的更换频率,进而对环境更友好。
技术原理

三相交流电或者单相交流电经工频整流滤波电路和功率因数校正电路变换成直流电,经高频逆变电路变换成高频交流电,注入到由谐振补偿电路和原边线圈构成的谐振网络,在原边线圈周围产生高频交变磁场,副边线圈在高频交变磁场中感应出高频交流电,经谐振补偿电路和整流滤波电路之后为电动汽车充电。
多阶段恒流充电
多阶段恒流充电示意图如图2所示,从图中可以看出充电过程分为若干个阶段,且从初始阶段到最终阶段电流是依次减小的,且电流越大,充电时间越短;电流越小,对应的阶段充电时间越长。


将动力电池的充电阶段分的越多,动力电池的充电电流便越接近于最佳充电曲线,对电池的损害便越小,更有利于延长动力电池的使用寿命。若动力电池为锂电池,最后阶段的电流一般为电池组容量的0.05倍,当电池电压达到截止电压便可以停止充电。
双LCC谐振补偿拓扑
如图3所示L1是原边线圈感值,L2是副边线圈感值,C1、Cf1和Lf1是原边补偿电感和电容,C2、Cf2和Lf2是副边补偿电感和电容,UAB是逆变器的输出电压和Uab是副边补偿拓扑的输出电压,M是原副边线圈互感。i1、i2、if1和if2分别是线圈L1、L2、Lf1、Lf2的电流。


电动汽车蓄电池充电机无线充电系统中的磁路机构是一个松耦合变压器,故可将图3中的副边电感电容折算到原边,得到如图4所示的等效电路图。为了简化分析,忽略电感电容的内阻,且只考虑逆变器输出电压的基波。定义松耦合变压器的变比n为:
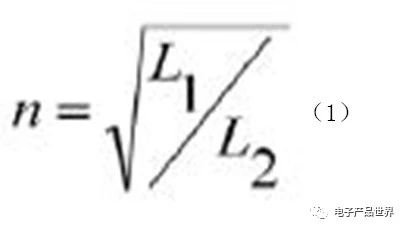
图4中的变量可由公式(2)表达:
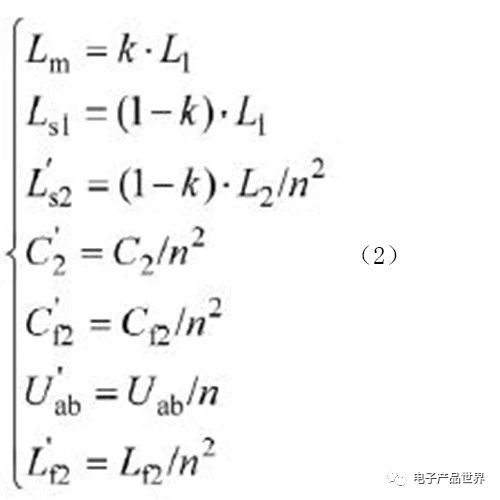
其中Lm为折算到原边的励磁电感。对于如图2所示的高阶系统,其谐振频率有多个,本文重点研究LCC的电压电流特性,不研究其频域特性,故本文将系统的工作频率设定为一个固定的谐振频率。电路谐振状态下,逆变器的输出电压和输出电流是同相位的,由公式(3)可计算电路的谐振频率。

此处的ω0是补偿电路的固有谐振角频率,从式(3)中可看出角频率只与电路中的电感电容有关,而与负载、原副边的互感无关。下文设定的频率均为固定的谐振角频率。
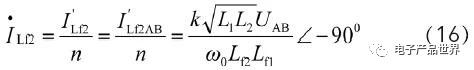



从式(3)可知,双LCC可以在动力电池充电的全过程以及耦合系数发生变化的情况下保持谐振状态,此性能非常符合电动汽车的蓄电池充电机无线充电的应用背景,因为动力电池充电过程中其等效电阻会不断增大,且每次充电原副边线圈会存在不同程度的偏移,故每次充电的耦合系数也是不同的。
由式(16)可知,双LCC补偿拓客可以实现恒流输出,且其输出电流的大小与逆变器的输出电压成正比,故可控制逆变器的输出电压来调节动力电池的充电电流,实现动力电池的多阶段恒流充电。
仿真验证
在MATLAB/Simulink中搭建仿真电路,电路参数表1所示。

图6为系统输出电流波形图。在0.06 s、0.1 s,0.14 s切换电阻,阻值依次为100 Ω、50 Ω、33 Ω及25 Ω,从图6中可得:电阻变化前后,电流几乎不变。电阻切换时出现震荡,在短时间内会稳定在某一固定值。动力电池充电时,可认为其等效内阻在一定时间内不变,故不会产生图7中所示的震荡。

图8为动力电池组不同的电量时对应的充电电流,因为在电脑中模拟的时间长度有限,故在仿真时每个阶段容量设置为0.005 C。

在t1时刻将电阻由25 Ω切换到33 Ω;在t2时刻将电阻由33 Ω切换到50 Ω,得到如图7所示的系统输出电流,可看出电阻切换前后电流大小几乎不变,可以用来实现电动汽车的多阶段恒流充电。
- 上一篇:充电机充电电池系统高压化的方案选择 2018/5/9
- 下一篇:高压大模组的全自动恒流恒压充电器充电蓄电池系统设计方案可行吗 2018/5/6
